晶振官方博客
更多>>Quartz Crystal建模的原理與操作
來源:http://tqlwapf.cn 作者:康華爾電子 2019年08月03
Quartz Crystal應(yīng)用已經(jīng)是非常廣泛了,人們研究并使用了一百多年,發(fā)展到今日超萬家專業(yè)晶振廠家的規(guī)模,為了使石英晶體的用處發(fā)揮到更大,眾多制造商和工程仍然在不斷的測試,鉆研,實(shí)驗(yàn)的去提升晶體晶振的性能.頻率頻段也從原來的KHz,MHz級(jí),更新到更高的GHz頻段,尺寸體積也越做越小,已有部分制造商成功開發(fā)出1.0*0.8mm大小的貼片晶振,融合了多種領(lǐng)先的技術(shù),建模方法就是其中一種.
本文章描述了一種具有負(fù)載電容的晶體建模方法.時(shí)鐘發(fā)生器(CLKgen)設(shè)計(jì)人員可以使用晶體模型輕松確定所需頻率的負(fù)載電容.電路和系統(tǒng)設(shè)計(jì)人員可以使用該模型來模擬晶體振蕩器的行為.為了模擬晶體,我們使用一個(gè)簡單的電路來測量不同負(fù)載電容下的振蕩頻率.然后,我們使用晶體電路模型來插值測量數(shù)據(jù)以確定電路模型中的參數(shù).
石英晶體已廣泛用于時(shí)鐘發(fā)生器和合成器,以產(chǎn)生精確的參考頻率.市場上最具成本效益的晶體頻率范圍為30kHz至30MHz,在0°C至70°C的溫度范圍內(nèi)精度為50-100ppm.要適當(dāng)?shù)厥褂没蛟O(shè)計(jì)石英晶體振蕩器,了解晶體在其負(fù)載條件下的行為非常重要.在本應(yīng)用筆記中,我們將介紹一種使用負(fù)載電容對(duì)晶體進(jìn)行建模的方法,并展示該模型的應(yīng)用.
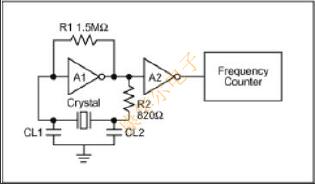
測試設(shè)置如圖1所示. 在設(shè)置中,A1和A2是逆變器;CL1和CL2是負(fù)載電容.在測試期間,CL1=CL2,當(dāng)變頻器電源電壓Vcc=3.1V且Vcc=2.3V時(shí),該值從5pf變化到59pf.測試中的晶振在負(fù)載電容為14pF時(shí)的標(biāo)稱頻率為27MHz.應(yīng)該注意,晶體的實(shí)際負(fù)載電容等于CL1||CL2加上板的寄生電容和逆變器的端子.
檢測結(jié)果
表1和2分別給出了Vcc=3.1V和2.3V的兩組測量值.
兩個(gè)測量數(shù)據(jù)集也繪制在圖2中
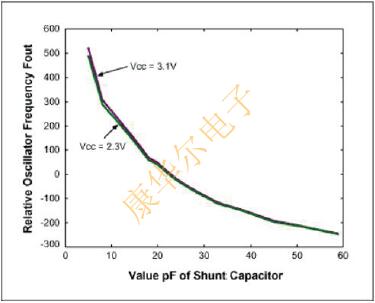
圖2.晶體頻率變化(ppm)與并聯(lián)電容值的關(guān)系.
從數(shù)據(jù)測量,我們有以下觀察:
1)負(fù)載電容可以顯著改變SMD晶振的振蕩頻率.結(jié)果表明,待測晶體的總晶體變化范圍可高達(dá)750ppm.
2)頻率變化也取決于Vcc.較低的電源電壓會(huì)降低頻率.這可能是由于電源電壓變化引起的逆變器輸入和輸出電容的變化.圖1中的電阻器R2具有降低這種電壓依賴性的作用.但電阻值不能太大;否則會(huì)使振蕩器難以啟動(dòng).
3)基于數(shù)據(jù),晶體頻率對(duì)小負(fù)載電容更敏感.這意味著在晶體振蕩器的應(yīng)用中,我們應(yīng)該使用需要相對(duì)較大負(fù)載電容的晶體作為其標(biāo)稱頻率.
4)圖1中的電阻器R1有助于振蕩器啟動(dòng).此外,逆變器的字符也會(huì)影響有源晶振的性能.應(yīng)使用高速逆變器.如果變頻器的速度不夠高,振蕩可能無法啟動(dòng).
石英晶體的建模
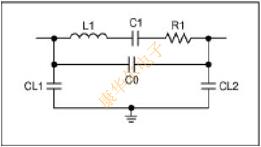
在振蕩器或VCXO設(shè)計(jì)中,需要晶體模型.通常采用的晶體諧振器模型[1-2]如圖3所示. 接下來,我們將使用表1和表2中給出的測量數(shù)據(jù)來確定圖3中元件的值.根據(jù)[1],在大多數(shù)晶體振蕩器應(yīng)用中,振蕩頻率是圖3中諧振器的并聯(lián)頻率.定義CL=CL1||CL2和fp為振蕩頻率,我們可以將阻抗方程寫成
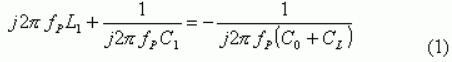
求解fP的等式,
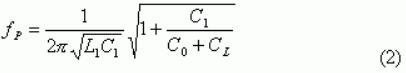
限定

然后我們可以重寫Eq.(2)以矢量形式表示
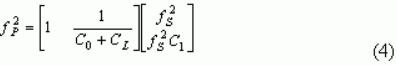
隨著Eq.(4)我們可以直接運(yùn)行最小二乘估計(jì)來估計(jì)fs,C1,L1和C0.應(yīng)注意,R1的值通常由晶體數(shù)據(jù)表給出.對(duì)于我們測試中使用的貼片晶振,R1=40Ω.為了估計(jì)C0,在給定電源電壓下,改變C0的值以獲得對(duì)測量數(shù)據(jù)集的最佳最小二乘擬合,假設(shè)Vcc的影響僅對(duì)C0的值.圖3中模型的估計(jì)組件值列出如下
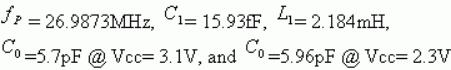
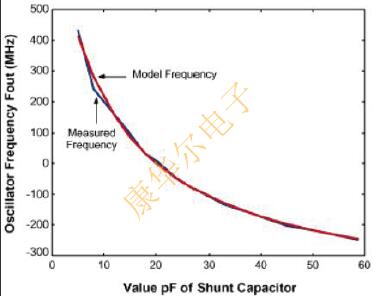
在圖4中,它顯示了由等式1計(jì)算的輸出頻率曲線.(2)估計(jì)的晶振元件值與測量的頻率相對(duì)應(yīng).對(duì)于Vcc=3.1V的情況,插值的均方根(RMS)為14ppm,對(duì)于Vcc=2.3V,插值的均方根為13ppm.
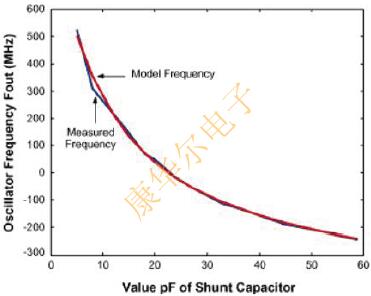
圖4a.最小二乘擬合數(shù)據(jù)集1(Vcc=3.1V),=5.7pF.
在本應(yīng)用筆記中,我們展示了一種用于測量石英晶體振蕩頻率的測試裝置和一種估算晶體諧振器模型參數(shù)的方法.實(shí)際測量揭示了振蕩頻率如何隨負(fù)載電容而變化.我們介紹了一種基于測量數(shù)據(jù)的數(shù)值方法,以估計(jì)石英晶體諧振器電路模型的參數(shù).如圖4所示,該模型與測量數(shù)據(jù)緊密匹配,均方根誤差(RMS)為13-14ppm.時(shí)鐘發(fā)生器設(shè)計(jì)人員可以使用該模型確定所需頻率的并聯(lián)電容值.系統(tǒng)和電路設(shè)計(jì)工程師可以使用該模型進(jìn)行系統(tǒng)行為模擬.
本文章描述了一種具有負(fù)載電容的晶體建模方法.時(shí)鐘發(fā)生器(CLKgen)設(shè)計(jì)人員可以使用晶體模型輕松確定所需頻率的負(fù)載電容.電路和系統(tǒng)設(shè)計(jì)人員可以使用該模型來模擬晶體振蕩器的行為.為了模擬晶體,我們使用一個(gè)簡單的電路來測量不同負(fù)載電容下的振蕩頻率.然后,我們使用晶體電路模型來插值測量數(shù)據(jù)以確定電路模型中的參數(shù).
石英晶體已廣泛用于時(shí)鐘發(fā)生器和合成器,以產(chǎn)生精確的參考頻率.市場上最具成本效益的晶體頻率范圍為30kHz至30MHz,在0°C至70°C的溫度范圍內(nèi)精度為50-100ppm.要適當(dāng)?shù)厥褂没蛟O(shè)計(jì)石英晶體振蕩器,了解晶體在其負(fù)載條件下的行為非常重要.在本應(yīng)用筆記中,我們將介紹一種使用負(fù)載電容對(duì)晶體進(jìn)行建模的方法,并展示該模型的應(yīng)用.
測試設(shè)置如圖1所示. 在設(shè)置中,A1和A2是逆變器;CL1和CL2是負(fù)載電容.在測試期間,CL1=CL2,當(dāng)變頻器電源電壓Vcc=3.1V且Vcc=2.3V時(shí),該值從5pf變化到59pf.測試中的晶振在負(fù)載電容為14pF時(shí)的標(biāo)稱頻率為27MHz.應(yīng)該注意,晶體的實(shí)際負(fù)載電容等于CL1||CL2加上板的寄生電容和逆變器的端子.
檢測結(jié)果
表1和2分別給出了Vcc=3.1V和2.3V的兩組測量值.
表1.Vcc=3.1V時(shí)可變負(fù)載電容的振蕩器頻率
| CL1,CL2(pf) | 五 | 8 | 12 | 15 | 18 | 20 | 22 |
| Fout(MHz) | 27.01411 | 27.00832 | 27.00583 | 27.00395 | 27.00188 | 27.00130 | 27.00037 |
| △Fout(ppm) | 523 | 308 | 216 | 146 | 70 | 48 | 14 |
| CL1,CL2(pf) | 24 | 27 | 33 | 39 | 45 | 50 | 59 |
| Fout(MHz) | 26.99954 | 26.99856 | 26.99687 | 26.99592 | 26.99480 | 26.99424 | 26.99340 |
| △Fout(ppm) | 17 | 53 | 116 | 151 | 193 | 213 | 244 |
表2.Vcc=2.3V時(shí)可變負(fù)載電容的振蕩器頻率
| CL1,CL2(pf) | 五 | 8 | 12 | 15 | 18 | 20 | 22 |
| Fout(MHz) | 27.01319 | 27.00780 | 27.00542 | 27.00360 | 27.00160 | 27.00106 | 27.00016 |
| △Fout(ppm) | 489 | 288 | 200 | 133 | 59 | 39 | 6 |
| CL1,CL2(pf) | 24 | 27 | 33 | 39 | 45 | 50 | 59 |
| Fout(MHz) | 26.99935 | 26.99837 | 26.99675 | 26.99579 | 26.99468 | 26.99415 | 26.99329 |
| △Fout(ppm) | -24 | -60 | -121 | -156 | -197 | -217 | -249 |

圖2.晶體頻率變化(ppm)與并聯(lián)電容值的關(guān)系.
1)負(fù)載電容可以顯著改變SMD晶振的振蕩頻率.結(jié)果表明,待測晶體的總晶體變化范圍可高達(dá)750ppm.
2)頻率變化也取決于Vcc.較低的電源電壓會(huì)降低頻率.這可能是由于電源電壓變化引起的逆變器輸入和輸出電容的變化.圖1中的電阻器R2具有降低這種電壓依賴性的作用.但電阻值不能太大;否則會(huì)使振蕩器難以啟動(dòng).
3)基于數(shù)據(jù),晶體頻率對(duì)小負(fù)載電容更敏感.這意味著在晶體振蕩器的應(yīng)用中,我們應(yīng)該使用需要相對(duì)較大負(fù)載電容的晶體作為其標(biāo)稱頻率.
4)圖1中的電阻器R1有助于振蕩器啟動(dòng).此外,逆變器的字符也會(huì)影響有源晶振的性能.應(yīng)使用高速逆變器.如果變頻器的速度不夠高,振蕩可能無法啟動(dòng).
石英晶體的建模
在振蕩器或VCXO設(shè)計(jì)中,需要晶體模型.通常采用的晶體諧振器模型[1-2]如圖3所示. 接下來,我們將使用表1和表2中給出的測量數(shù)據(jù)來確定圖3中元件的值.根據(jù)[1],在大多數(shù)晶體振蕩器應(yīng)用中,振蕩頻率是圖3中諧振器的并聯(lián)頻率.定義CL=CL1||CL2和fp為振蕩頻率,我們可以將阻抗方程寫成
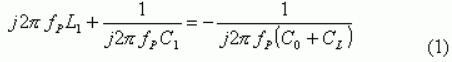
求解fP的等式,
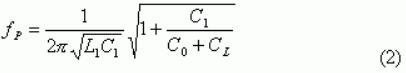
限定

然后我們可以重寫Eq.(2)以矢量形式表示
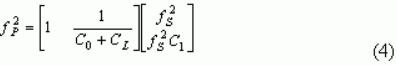
隨著Eq.(4)我們可以直接運(yùn)行最小二乘估計(jì)來估計(jì)fs,C1,L1和C0.應(yīng)注意,R1的值通常由晶體數(shù)據(jù)表給出.對(duì)于我們測試中使用的貼片晶振,R1=40Ω.為了估計(jì)C0,在給定電源電壓下,改變C0的值以獲得對(duì)測量數(shù)據(jù)集的最佳最小二乘擬合,假設(shè)Vcc的影響僅對(duì)C0的值.圖3中模型的估計(jì)組件值列出如下
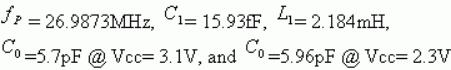
在圖4中,它顯示了由等式1計(jì)算的輸出頻率曲線.(2)估計(jì)的晶振元件值與測量的頻率相對(duì)應(yīng).對(duì)于Vcc=3.1V的情況,插值的均方根(RMS)為14ppm,對(duì)于Vcc=2.3V,插值的均方根為13ppm.

圖4a.最小二乘擬合數(shù)據(jù)集1(Vcc=3.1V),=5.7pF.
正在載入評(píng)論數(shù)據(jù)...
相關(guān)資訊
- [2023-09-26]臺(tái)灣SIWARD晶振有著領(lǐng)先全球的光蝕刻制...
- [2023-07-12]淺談決定差分石英晶體振蕩器的振蕩頻率...
- [2023-06-27]SMD時(shí)鐘硅振蕩器從0/+70°c到-55/+125°...
- [2023-06-20]GPS接收器專用溫補(bǔ)晶體振蕩器C34-040.0...
- [2023-06-17]Cardinal石英晶體CSM1Z-A5B2C5-40-25.0...
- [2023-06-13]Aker音叉晶體CTS3-32.768-9-20-R為何開...
- [2023-02-16]具備高品質(zhì)的石英晶體用于無線通信CS-0...
- [2022-09-16]EPSON蘋果手機(jī)無線充電器專用晶振Q3805...
- [2022-08-04]Abracon生產(chǎn)非常適合微處理器的時(shí)鐘晶體...
- [2022-08-03]西迪斯設(shè)計(jì)出獨(dú)特性能的小型化時(shí)鐘振蕩...
- [2022-08-02]村田首推用于消費(fèi)級(jí)的陶瓷諧振器CSTLS8...
- [2022-07-22]常用編碼KC3225K12.0000C1GE00是一款微...



 銷售代表
銷售代表 售后服務(wù)
售后服務(wù)
.jpg)
.jpg)